Зміст
У вас бувало таке, що під час прогулянки ви зависли в телефоні і в результаті «врізалися» в якусь тверду річ, наприклад, у дорожній знак? У мене бувало. Це боляче і дуже безглуздо. У тому, що нам боляче врізатись у тверді предмети, винна сила нормальної реакції (або нормальна реакція опори).
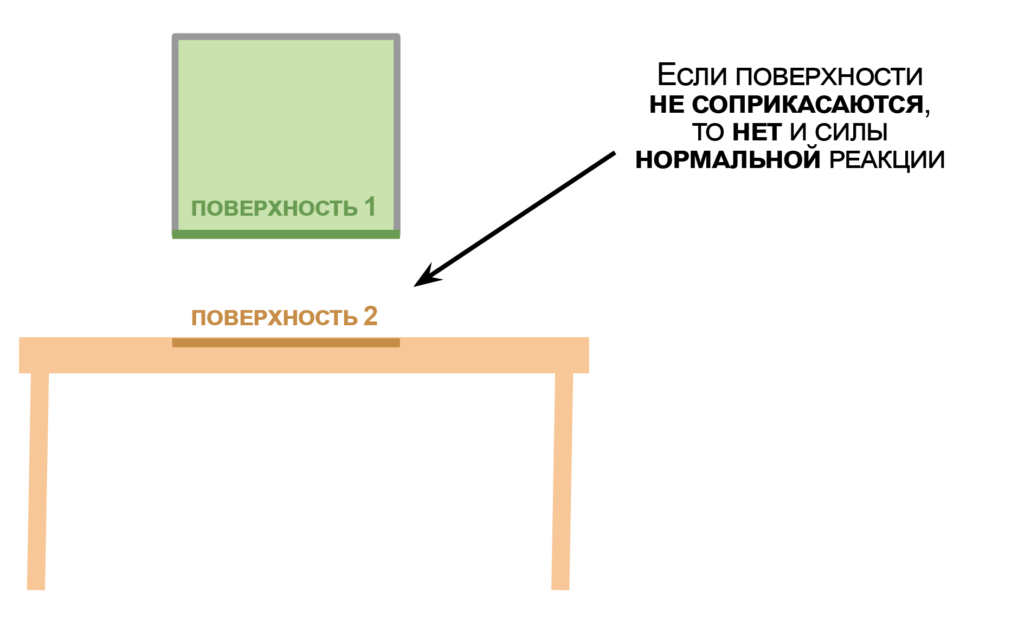
Сила нормальної реакції – це сила, яка перешкоджає твердим тілам проходити один крізь одного.Сила нормальної реакції виникає внаслідок зіткнення. Якщо поверхні не стикаються одна з одною, сили нормальної реакції між ними немає. Наприклад, якщо поверхні столу та ящика не стикаються, то вони і не впливають одна на одну силою нормальної реакції.

Але якщо поверхні стикаються (наприклад, ящик і стіл), тоді вони впливають один на одного силою нормальної реакції, перпендикулярної площині поверхонь, що стикаються. Ця сила тим більше, чим сильніше поверхні тіл опираються «проходженню» через одне одного. Чому на ілюстрації нижче стіл здається вигнутим?

Слово “нормальний” у вираженні сила нормальної реакції не означає “звичайний” або “природний”. Тут “нормальний” – це синонім слова перпендикулярний , оскільки сила нормальної реакції, що часто позначається як FnF, start subscript, n, end subscriptабо просто NN, спрямована перпендикулярно дотичних поверхонь. Це логічно, тому що сила нормальної реакції перешкоджає поверхням пройти через один одного. Існують інші сили, що виникають внаслідок зіткнення, наприклад, коли тіла рухаються паралельно одна одній, але в такому випадку вони називаються силами тертя, оскільки вони перешкоджають ковзанню поверхонь одна про одну.
Як неживі предмети «знають», що потрібно докласти сили нормальної реакції?
Багатьом очевидно, що коли несеш важкий пакет із собачим кормом, як у малюнку 3(a) нижче, потрібно докласти силу, спрямовану вгору. Але важко уявити, що неживі предмети, такі як стіл, можуть прикладати до того ж пакету собачого корму спрямовану вгору силу нормальної реакції, як показано на малюнку 3(b).
Декому здається, що стіл взагалі не прикладає до пакета спрямовану вгору силу, він просто «заважає» йому впасти на підлогу. Але це суперечить законам Ньютона. Якби на пакет вплинула лише сила тяжіння Землі, пакет рухався б униз із прискоренням. Столу мало просто «підтримувати пакет», щоб він не впав, стіл повинен впливати на пакет із силою, спрямованою нагору.
Дивно, але якщо на стіл покласти важчий предмет і для того, щоб цей предмет не впав, стіл повинен впливати на нього з більшою силою нормальної реакції. Як стіл «знає», яку силу треба прикласти, щоб запобігти падінню тіла крізь стіл? По суті, стіл «дізнається», яку силу потрібно докласти, залежно від того, наскільки сильно деформується його поверхня.
Коли тверді предмети викривляються, вони намагаються повернутись до своєї природної форми. Що більше вантаж, то більше вписувалося деформація, і більше сили всередині стільниці намагаються повернути їх у природне становище. Таку деформацію можна помітити неозброєним оком, якщо покласти на картковий стіл досить важкий вантаж, хоча, правду кажучи, будь-які, навіть найтвердіші предмети викривляються, якщо прикласти до них силу.
Поки предмет не деформований до певної межі, внутрішні сили в ньому намагатимуться повернути його в початкову форму, подібно до пружини, батуту або трампліну для стрибків у воду.
Тому, якщо помістити на стіл вантаж, стільниця прогинатиметься, поки сили, що відновлюють, не зрівняються з вагою вантажу. У цей момент результуюча сила, що діє на вантаж, дорівнюватиме нулю. У такій ситуації вантаж на столі перебуватиме у стані спокою. Зазвичай стільниця прогинається дуже швидко, а сама деформація незначна, тому часто не помічаємо цього процесу.

Малюнок 3. (a) Людина, яка тримає пакет із собачим кормом, повинна прикладати до неї силу рукFрукF, start subscript, start text, р, у, k, end text, end subscript, рівну за величиною і протилежну за вагою пакету WW. (b) Картковий стіл прогинається під пакетом собачого корму, як батут. Сила пружності, що виникає в столі, зростає, доки не стане рівною силі нормальної реакції NNабо FnF, start subscript, n, end subscript, що дорівнює за величиною та протилежною за напрямом ваги вантажу. (Джерело зображення: Openstax College Physics)
Як знайти силу нормальної реакції?

Для сили нормальної реакції немає окремої формули. Щоб обчислити силу нормальної реакції, як правило, використовуються дані про прискорення, спрямоване перпендикулярно до поверхонь (оскільки ми припускаємо, що поверхні не можуть «проходити» один через одного). Отже, знаходження сили нормальної реакції опори майже завжди використовується другий закон Ньютона.
- Малюємо схему, де відображаємо всі сили, що діють на предмет, що цікавить нас.
- Як напрям для застосування другого закону Ньютона вибираємо напрям сили нормальної реакції, тобто перпендикуляр до поверхонь, що стикаються.
- Підставимо прискорення, масу та чинні сили у формулу другого закону Ньютона(=Σ)( a=mΣ F)left parenthesis, a, equals, start fraction, Sigma, F, divided by, m, end fraction, right parenthesisдля цього напряму.
- Знаходимо силу нормальної реакції FnF, start subscript, n, end subscript.
Фактично ми знаходимо силу нормальної реакції, припускаючи, що вона дорівнює силі, що перешкоджає поверхням «проходити» один через одного.Давайте розглянемо цю стратегію простому прикладі. Нехай на столі в стані спокою лежить тіло масою mm, як показано нижче.


Сила нормальної реакції не завжди дорівнюватиме m gm, g. Якщо розглянути більш складний випадок, наприклад, коли поверхні, що стикаються, не горизонтальні, або коли на тіла впливають інші сили, або існує ненульове вертикальне прискорення, сила нормальної реакції може не дорівнювати m gm, g. Однак навіть для складніших випадків ми все одно знаходитимемо її за описаним вище алгоритмом. Можливо, нам доведеться підставляти інше значення прискорення або враховувати інші сили, але загальний принцип знаходження сили нормальної реакції за другим законом Ньютона залишиться тим самим.
Як вирішуються завдання на силу нормальної реакції?
Приклад 1. Сила нормальної реакції ліфта
Упаковка жувальної гумки зі смаком ківі масою4,5 кг4 , 5 кг 4, comma, 5, start text, space, k, г, end textдоставляється на верхній поверх офісної будівлі. Ящик стоїть на підлозі ліфта, що рухається вгору із прискоренням=3,0мз2a=3 , 0з2мa, equals, 3, comma, 0, start fraction, start text, м, end text, divided by, start text, c, end text, squared, end fraction. Кур’єр поставив на нього одну ногу, впливаючи на ящик спрямованою вниз силою5 Н5 Н 5, start text, space, Н, end text.Чому дорівнює сила нормальної реакції статі ліфта, що діє на ящик?Насамперед ми малюємо схему, на якій позначаємо всі сили, що діють на скриньку. На цій схемі ми не відображаємо прискорення, оскільки прискорення це не сила. Крім того, ми також не відбиваємо на ній додаткову силу з боку ліфта , оскільки сила нормальної реакції — це сила , що діє з боку ліфта на ящик. (Ми використовуємо другий закон Ньютона у вертикальному напрямку)

Зверніть увагу, що якби ми, не замислюючись, використовували формулу=44,1 НFn=m g=4 4 , 1 Н F, start subscript, n, end subscript, equals, m, g, equals, 44, comma, 1, start text, space, Н, end textтоді ми отримали б неправильну відповідь. В даному випадку сила нормальної реакції відрізняється від m gm, g, оскільки є вертикальне прискорення і додаткова вертикальна сила.
Приклад 2. Сила нормальної реакції з діагональною силою
Людина штовхає коробку з шоколадно-м’ятним печивом масою1,0 кг1 , 0 кг 1, comma, 0, start text, space, k, г, end textпо абсолютно гладкому столу (без сили тертя), застосовуючи силу=10 НFA=1 0 Н F, start subscript, A, end subscript, equals, 10, start text, space, Н, end text, спрямовану діагонально під кутом=30θ=3 0otheta, equals, 30, start superscript, o, end superscript, як показано нижче.Чому дорівнює сила нормальної реакції столу, яка діє коробку?
Незважаючи на те, що завдання здається зовсім несхожим на попереднє, проте принцип його вирішення буде таким самим. Спершу малюємо схему всіх сил, прикладених до коробки.
Формула розрахунку сили реакції опори

Розрахунок реакцій відноситься до розділу фізики з назвою “Статика”, яка розглядає структуру та системи, що перебувають у спокої.
Силою реакції опори називається зусилля протидії опори об’єкту, що діє на неї, при цьому вона дорівнює по модулю і протилежна за напрямом зусилля, з яким об’єкт діє на опору, згідно з третім законом Ньютона.
Система між деякою структурою та опорою, яка перешкоджає лінійному або кутовому переміщенню цієї структури, називається системою опори. Існує кілька типів опор:
- Шарнір (валик) – опора першого порядку, що обмежує зміщення в просторі в одному вимірі і має реакцію опори перпендикулярної основи.
- Плоска опора – опора другого порядку, яка обмежує переміщення у просторі у двох вимірах (горизонтальному та вертикальному) і дозволяє лише рух обертання структури.
Розрахунок рівноважних систем пов’язані з обчисленням результуючого динамічного моменту. У ньютонівській (класичній) механіці момент сили визначається як векторний добуток зусилля, що діє на опору, на вектор, утворений між точкою опори та точкою докладання цього зусилля. Момент сили називають динамічним моментом або просто моментом.
Далі у статті наводиться приклад розрахунку реакції для найпоширенішого завдання: балки з двома опорами.

Розв’язання задачі про реакцію опори балки
Як було сказано вище, балка з двома опорами є типовим і найпростішим завданням статики. Завдання полягає у розрахунку реакцій у точках А і В через діючі на балку зусилля.
Знання цих величин необхідне правильного розуміння діаграм моментів і діаграм сил цієї системи, і є важливою частиною статики у шкільних та університетських курсах. Існує комп’ютерна програма SkyCiv , яка надає потужний інструмент для розрахунку таких реакцій для різних рівноважних систем.
Повертаючись до поставленого вище завдання, нагадаємо, що основною її умовою є статичний стан, тобто відсутність будь-яких лінійних переміщень та обертань об’єктів. У простій фізиці останній факт означає, що сума векторів усіх зусиль дорівнює нулю (тобто сума зусиль, спрямованих нагору, дорівнює таким, спрямованим донизу). Другою умовою рівноваги системи є рівність нуля динамічних моментів, доданих щодо певної точки опори.
Щоб визначити реакції підпорок балки, дотримуйтеся двох способів розв’язання задачі:
- використовуючи рівність нулю суми динамічних моментів;
- використовуючи рівність нулю суми діючих зусиль.

Перший спосіб: через моменти
Спочатку потрібно покласти, що сума всіх моментів щодо точки реакції дорівнює нулю, тобто ΣMi = 0, де Мi – момент зусилля. Розрахунок таких моментів для нашого завдання дуже простий, і полягає у перемноженні діючих зусиль на відстані від точки їх застосування до точки реакції.
Вважатимемо, що наша балка має довжину 4 метри і розташована на двох підпірках А і В. Посередині балки вертикально вниз діє зусилля в 20 кН, і потрібно розрахувати реакції кожної підпірки, тобто Ay і By. Описана задача представлена малюнку.

Наприклад, розрахуємо суму всіх динамічних моментів щодо точки реакції, враховуючи її рівність нулю в рівновазі. Вибір точки, щодо якої буде проводитися розрахунок, є довільним, так само можна вибрати точку А. Таким чином, підсумуємо всі динамічні моменти щодо точки, вважаючи цю суму рівною нулю:
ΣMв = 0 = 20 * 2 – A y * 4 = => A y = 10 кН.
Зазначимо, що у формулі вище ми вибрали позитивний напрямок для моментів, що діють проти годинникової стрілки, та негативний напрямок для моментів, що діють за годинниковою стрілкою. Такий вибір символів момент є найбільш загальним, однак, ви можете вибрати і навпаки. Необхідно пам’ятати, що завжди потрібно використовувати одну й ту саму угоду на знак моментів, починаючи спочатку і слідуючи їй протягом усього вирішення конкретного завдання.
Таким чином, ми отримали нашу першу формулу, з якої визначили силу реакції опори в точці А. Аналогічна формула запишеться для визначення реакції в точці В. У нашому випадку, зважаючи на симетричність діючого вертикально вниз зусилля в 20 кН щодо точок підпірок, реакція в точці В буде дорівнює такій в точці А.
Другий спосіб: через сили
Для існування рівноваги сума всіх вертикальних сил повинна дорівнювати нулю, тобто ΣF y = 0, де індекс Y визначає конкретну вертикальну силу в системі. Пам’ятайте, що в даному випадку ми повинні включати до уваги всі чинні в системі сили. Беручи до уваги останній факт, проводимо підсумовування всіх вертикальних сил, у результаті отримуємо таку формулу:
ΣF y = 0 = A y + Y – 20 кН, звідки 0 = 10 кН + Y – 20 кН, і Y = 10 кН.
Так само, як і у разі моментів сил, сили є векторними величинами та мають знак, тут ми прийняли за позитивні сили ті, що діють вгору, та за негативні ті, що діють вниз. Вибір знака залишається за вами, проте нагадуємо, що цей вибір не повинен змінюватися в процесі вирішення завдання. Зазначимо, що у вище формулі ми використовували результат, отриманий у попередньому пункті, коли обчислили силу реакції Ay.

Таким чином, ми вирішили, поставлену на початку цього параграфа задачу про розрахунок сил реакцій опори балки, використовуючи при цьому дві системи рівнянь, рівняння моменту сили та рівняння сили, та отримали відповіді: сили реакції в точках А і В рівні між собою і становлять 10 кН. Нагадуємо, що фізичний зміст отриманої рівності полягає в тому, що зовнішня сила, що діє на балку, прикладена точно посередині балки. У разі її застосування в іншій точці наведені формули також будуть дійсні і процес розрахунку залишається тим самим.
Архіви
- Лютий 2026
- Січень 2026
- Грудень 2025
- Листопад 2025
- Жовтень 2025
- Вересень 2025
- Серпень 2025
- Липень 2025
- Червень 2025
- Травень 2025
- Квітень 2025
- Березень 2025
- Лютий 2025
- Січень 2025
- Грудень 2024
- Листопад 2024
- Жовтень 2024
- Вересень 2024
- Серпень 2024
- Липень 2024
- Червень 2024
- Травень 2024
- Квітень 2024
- Березень 2024
- Лютий 2024
- Листопад 2023
- Жовтень 2023
- Вересень 2023
- Серпень 2023
- Липень 2023
- Червень 2023
- Травень 2023
- Квітень 2023
- Березень 2023
- Лютий 2023
- Січень 2023
- Грудень 2022
- Листопад 2022
- Жовтень 2022
- Вересень 2022
- Серпень 2022
- Липень 2022
- Червень 2022
- Травень 2022
- Квітень 2022
- Березень 2022
- Лютий 2022
- Січень 2022
- Грудень 2021
- Листопад 2021
- Жовтень 2021
- Вересень 2021
- Серпень 2021
- Липень 2021
- Червень 2021
- Травень 2021
- Квітень 2021
- Березень 2021
- Лютий 2021
- Січень 2021
- Грудень 2020
- Листопад 2020
- Жовтень 2020
- Вересень 2020
- Серпень 2020
- Липень 2020
- Червень 2020
- Травень 2020
- Квітень 2020
- Березень 2020
- Лютий 2020
- Січень 2020
- Грудень 2019
Calendar
| Пн | Вт | Ср | Чт | Пт | Сб | Нд |
|---|---|---|---|---|---|---|
| 1 | ||||||
| 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 9 | 10 | 11 | 12 | 13 | 14 | 15 |
| 16 | 17 | 18 | 19 | 20 | 21 | 22 |
| 23 | 24 | 25 | 26 | 27 | 28 | 29 |
| 30 | 31 | |||||