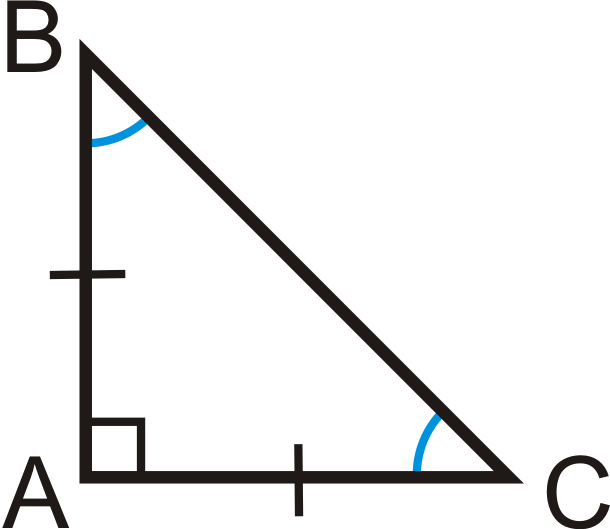
Прямокутний трикутник: що це таке, головні властивості та як швидко розв’язувати задачі
Зміст
- 1 Як виглядає прямокутний трикутник і як називаються його сторони
- 2 Властивості прямокутного трикутника, які рятують на контрольній
- 3 Прямокутний трикутник і теорема Піфагора: головна формула
- 4 Найпопулярніші «готові» трикутники: щоб рахувати швидше
- 5 Площа прямокутного трикутника: проста формула без сюрпризів
- 6 Коли треба синуси й косинуси: без страху, по-людськи
- 7 Типові помилки, які роблять навіть розумні люди
- 8 Міні-шпаргалка: що корисно мати перед очима
- 9 FAQ: що найчастіше питають у Google про прямокутні трикутники
Прямокутний трикутник — це трикутник, у якого один кут дорівнює 90°, а дві сторони, що утворюють цей кут, називаються катетами. Сторона навпроти прямого кута — гіпотенуза, і вона завжди найдовша.
Якщо хочеш розібратися ще простіше й з прикладами «на пальцях», ось корисний матеріал: прямокутний трикутник: властивості, формули та приклади простими словами.
Якщо коротко: усе «магічне» у цьому трикутнику крутиться навколо прямого кута, катетів і гіпотенузи — а далі вже працюють чіткі формули.
Як виглядає прямокутний трикутник і як називаються його сторони
У прямокутному трикутнику є три ключові елементи:
- прямий кут (90°) — головна ознака;
- два катети — сторони, що утворюють прямий кут;
- гіпотенуза — сторона навпроти прямого кута.
Уяви найпростішу ситуацію з життя: драбина, приставлена до стіни. Підлога і стіна утворюють прямий кут, а драбина — це гіпотенуза. Ось тобі й готова «модель» трикутника без підручника.
Властивості прямокутного трикутника, які рятують на контрольній
Прямокутні трикутники люблять за те, що вони передбачувані: є кілька правил, які працюють майже завжди.
Гіпотенуза завжди найбільша
Звучить банально, але це реально допомагає, коли в задачі треба швидко зрозуміти, яка сторона яка. Якщо бачиш три числа — найбільше майже завжди претендує на роль гіпотенузи (але краще перевірити формулою).
Сума гострих кутів — 90°
У будь-якому трикутнику сума кутів 180°. Якщо один 90°, то два інші разом дадуть теж 90°.
Тобто якщо один гострий кут 35°, то інший буде 55°. Без магії, просто арифметика.
Медіана до гіпотенузи — це половина гіпотенузи
У прямокутному трикутнику середина гіпотенузи однаково віддалена від усіх трьох вершин. Звідси корисне правило:
медіана, проведена з прямого кута до гіпотенузи, дорівнює половині гіпотенузи.
Це люблять запихати в задачі, де треба «побачити» розв’язок, а не рахувати 10 рядків.
Прямокутний трикутник і теорема Піфагора: головна формула
Ось тут уже без варіантів. Якщо в задачі є прямий кут — майже напевно десь поруч стоїть Піфагор.
Теорема Піфагора:
a2+b2=c2a^2 + b^2 = c^2a2+b2=c2
де a і b — катети, а c — гіпотенуза.
Як це працює на прикладі
Катети 3 і 4. Знайдемо гіпотенузу:
c=32+42=9+16=25=5c = \sqrt{3^2 + 4^2} = \sqrt{9 + 16} = \sqrt{25} = 5c=32+42=9+16=25=5
Це класична трійка чисел 3–4–5, і вона зустрічається настільки часто, що її варто запам’ятати як пароль від Wi-Fi.
Найпопулярніші «готові» трикутники: щоб рахувати швидше
Є набори чисел, які дуже часто випадають у задачах. Їх називають піфагоровими трійками.
Ось кілька найвідоміших:
- 3–4–5
- 5–12–13
- 8–15–17
- 7–24–25
Якщо бачиш щось схоже — є шанс, що задача вирішиться буквально за 10 секунд.
Площа прямокутного трикутника: проста формула без сюрпризів
У звичайному трикутнику площа — це половина добутку основи на висоту.
А тут усе ще легше, бо катети вже самі «грають роль» основи й висоти.
S=a⋅b2S = \frac{a \cdot b}{2}S=2a⋅b
Наприклад, якщо катети 6 і 8:
S=6⋅82=24S = \frac{6 \cdot 8}{2} = 24S=26⋅8=24
Коли треба синуси й косинуси: без страху, по-людськи
Тригонометрія звучить грізно, але в прямокутному трикутнику вона максимально логічна.
Для гострого кута α\alphaα:
\sin(\alpha) = \frac{\text{протилежний катет}}{\text{гіпотенуза}}
]
\cos(\alpha) = \frac{\text{прилеглий катет}}{\text{гіпотенуза}}
]
\tan(\alpha) = \frac{\text{протилежний катет}}{\text{прилеглий катет}}
]
Як не переплутати
Дивишся на кут.
Сторона навпроти нього — «протилежна», та що поруч — «прилегла».
Гіпотенуза завжди одна — найбільша і навпроти 90°.
Типові помилки, які роблять навіть розумні люди
Іноді задача проста, але помилка робить її «нервовою». Ось найчастіше:
- Плутають гіпотенузу з катетом
Гіпотенуза — тільки навпроти прямого кута. Завжди. - Неправильно підставляють у Піфагора
Формула не «найбільше² + найменше²», а саме:
катет² + катет² = гіпотенуза². - Забувають про корінь
Якщо знайшов c2=49c^2 = 49c2=49, то c=7c = 7c=7, а не 49. Таке трапляється частіше, ніж здається.
Міні-шпаргалка: що корисно мати перед очима
| Що шукаємо | Формула |
|---|---|
| Гіпотенуза | c=a2+b2c=\sqrt{a^2+b^2}c=a2+b2 |
| Катет | a=c2−b2a=\sqrt{c^2-b^2}a=c2−b2 або b=c2−a2b=\sqrt{c^2-a^2}b=c2−a2 |
| Площа | S=a⋅b2S=\frac{a\cdot b}{2}S=2a⋅b |
| Синус | sin(α)=ac\sin(\alpha)=\frac{a}{c}sin(α)=ca |
| Косинус | cos(α)=bc\cos(\alpha)=\frac{b}{c}cos(α)=cb |
| Тангенс | tan(α)=ab\tan(\alpha)=\frac{a}{b}tan(α)=ba |
FAQ: що найчастіше питають у Google про прямокутні трикутники
1) Як зрозуміти, що трикутник прямокутний?
Якщо один кут 90° — він прямокутний.
Або якщо виконується теорема Піфагора: a2+b2=c2a^2+b^2=c^2a2+b2=c2.
2) Чому гіпотенуза завжди найдовша?
Бо вона лежить навпроти найбільшого кута (90°). У геометрії найбільший кут — найбільша сторона.
3) Чи може у прямокутного трикутника бути два прямі кути?
Ні. Сума кутів трикутника 180°, два по 90° вже дали б 180° — а третій кут тоді був би 0°, тобто трикутник «зник».
4) Як знайти площу, якщо відома гіпотенуза і кут?
Можна знайти катети через синус і косинус, а потім використати S=a⋅b2S=\frac{a\cdot b}{2}S=2a⋅b.
5) Чи буває прямокутний рівнобедрений трикутник?
Так. Якщо катети рівні, то гострі кути будуть по 45°. Це дуже популярний тип задач.
Прямокутний трикутник — один із найзручніших «інструментів» у геометрії: все чітко, формули працюють стабільно, а задачі часто вирішуються за кілька кроків. Якщо запам’ятати, де катети, де гіпотенуза, і тримати в голові Піфагора — половина завдань перестає бути страшною. А коли підключаєш площу та тригонометрію, стає зрозуміло: цей трикутник не складний, він просто дуже популярний.