Закон збереження імпульсу – Який закон збереження імпульсу?
Зміст
Імпульс тіла, що рухається дорівнює добутку його маси на швидкість.
Повний імпульс замкнутої системи зберігається. Цей закон був встановлений для тіл, що сударяються, в 1668 році Джоном Валлісом, Крістофером Реном і Християном Гюйгенсом.
Закон збереження імпульсу пояснює віддачу рушниці та дозволяє її розрахувати. Шкільна фізика в дослідах та експериментах. Дивіться, як ми робимо досліди з фізики, робіть їх разом із нами, вигадуйте та показуйте нові досліди. Слухайте наші міркування, розбирайтеся в них, вигадуйте свої пояснення та робіть свої розрахунки. Це найкращий спосіб зрозуміти, як працює фізика!
Імпульс. Закон збереження імпульсу.
При вирішенні динамічних завдань необхідно знати, які сили діють на тіло, закон, що дозволяє розрахувати конкретну силу. Мета: отримати розв’язання задачі механіки виходячи з початкових умов, не знаючи конкретного виду взаємодії.
Закони Ньютона в отриманій раніше формі не дозволяють вирішувати задачі на рух тіла зі змінною масою та при швидкостях, порівнянних зі швидкістю світла. Мета : отримати записи законів Ньютона у формі, справедливої цих умов.
Імпульс сили Векторна фізична величина є мірою дії сили за деякий проміжок часу. – Імпульс сили за малий проміжок часу t.
Вектор імпульсу сили направлені з вектор сили.
[I] = Н. з
Імпульс тіла. (Кількість руху) Векторна фізична величина, що є мірою механічного руху і дорівнює добутку маси тіла на його швидкість.
Вектор імпульсу тіла направлений з вектором швидкості тіла.
[ p ]= кг м/с
Основне рівняння динаміки
Із другого закону Ньютона:
Тоді отримаємо:
Другий закон Ньютона в
(Dt = t – t 0 = t при t 0 = 0).
Імпульс сили дорівнює зміні імпульсу тіла . Вектор імпульсу сили та зміни імпульсу тіла співспрямовані.
Непружний удар (кулька “прилипає” до стінки):
Абсолютно пружний удар (кулька відскакує з колишньою за величиною швидкістю):
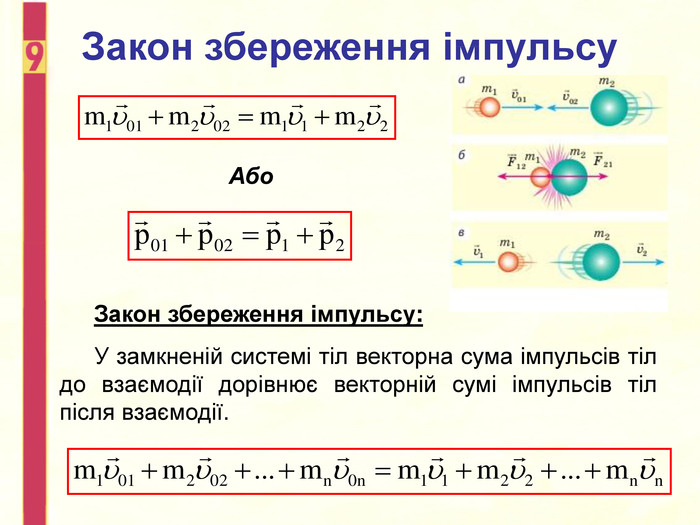
Закон збереження імпульсу.
До взаємодії
Після взаємодії
Відповідно до 3 з-ну Ньютона:
отже:
Геометрична (векторна) сума імпульсів взаємодіючих тіл, що становлять замкнуту систему, залишається незмінною .
Замкнутою називається система тіл, що взаємодіють лише один з одним і не взаємодіють з іншими тілами. Можна користуватися і для незамкнутих систем, якщо сума зовнішніх сил, що діють на тіла системи, дорівнює нулю, або процес відбувається дуже швидко, коли зовнішніми впливами можна знехтувати (вибух, атомні процеси).
Загалом: т.к. система замкнута, то
отже
Приклади застосування закону збереження імпульсу:
- Будь-які зіткнення тіл (біліардних куль, автомобілів, елементарних частинок тощо);
- Рух повітряної кульки при виході з неї повітря;
- Розриви тіл, постріли тощо.
Застосування закону збереження імпульсу у разі зіткнень частинок
Використовуючи закон збереження імпульсу, можна проаналізувати рух частинок при зіткненнях, не знаючи в подробицях сили, що діють між ними. Згодом ми побачимо, що зіткнення бувають різних типів. Деякі їх можна досліджувати остаточно, використовуючи лише закон збереження імпульсу, інші не можна. Проте й у випадках, припускаючи деякі додаткові властивості сил, вдається з’ясувати багато про рух тіл, не деталізуючи характеру сил.
Почнемо з найпростішого випадку руху вздовж одного напрямку. Уявимо дві частинки — для наочності, наприклад, дві більярдні кулі. (Незважаючи на наочність, порівняння з більярдними кулями на столі є дещо умовним, тому що кулі обертаються. Було б правильніше представляти два частковоподібні предмети — крижані шайби на поверхні замерзлого озера або більярдні кулі в міжпланетному просторі, — які тільки переміщуються в просторі, але не роблять інші рухи на зразок обертання, проте теорія зіткнень без більярдних куль, як і теорія ймовірності без рулетки, подібна до трапези без вина.
Уявімо дві більярдні кулі (спочатку тих, що покояться), які стосуються один одного, а потім розлітаються під дією сили, що виникає між ними. Нас не цікавить питання, що це за сила. Вона може з’явитися завдяки невеликому вибуху, пружині чи будь-якій іншій причині. Після вибуху кулі рухаються у різні боки одна від одної. Чи можна, не знаючи подробиць впливу, щось сказати, про рух куль після вибуху? Якби ми спробували відповісти на це питання, спираючись безпосередньо на закони Ньютона, нам слід точно знати силу, що діяла на більярдні кулі під час вибуху, що дуже важко, оскільки величина цієї сили досягає дуже великого значення за надзвичайно короткий проміжок часу і змінюється згодом за складним законом.Однак ми можемо впоратися із завданням, використовуючи закон збереження імпульсу.
Аналіз руху двох частинок рівної маси, які перебували в початковий момент у спокої
Перед вибухом (фіг. 102):
v 1 = 0, p 1 = mv 1 = 0, (11.22)
v 2 = 0, p 2 = mv 2 = 0, (11.23)
Отже, повний імпульс системи двох частинок
P = p 1 + p 2 = 0, (11.24)
Він залишається незмінним, як частинки, ні взаємодіяли між собою (фіг. 103, 104).
Будемо позначати (фіг. 104) швидкості після вибуху через v 1 `і v 2` . Після вибуху тіло 1 рухається зі швидкістю v 1 `, а тіло 2 – зі швидкістю v 2` . Між v 1 `і v 2 ` існує зв’язок, оскільки повний імпульс системи після вибуху, згідно з теоремою 11.2:
P ` = p 1 ` + p 2 ` = mv 1 ` + mv 2 ` = 0, (11.25)
(Імпульс системи після вибуху збігається з її імпульсом до вибуху, який дорівнював нулю). Отже,
mv 1 `+ mv 2` = 0, (11.26)
або
v 1 ` = – v 2 `
Таким чином, кулі розлітатимуться в різні боки з однаковою швидкістю незалежно від конкретних властивостей сили, що їх розділила. У загальному випадку багатьох частинок закон збереження імпульсу записується у вигляді одного рівняння, яке завжди виконується:
p 1 + p 2 + p 3 + … + p n = const
Іншими словами, повний імпульс системи залишається незмінним.
При вирішенні задачі, яку прийнято називати проблемою зіткнень, зазвичай говорять про початковий імпульс, або імпульс до зіткнення, і про кінцевий імпульс, або імпульс після зіткнення. При зіткненні частки, як правило, взаємодіють один з одним дуже короткий проміжок часу, протягом якого відбувається зміна їх імпульсів. Перед зіткненням усі частинки рухаються згідно з першим законом Ньютона, і після зіткнення їх рух знову підкоряється цьому закону. Імпульси частинок змінюються тільки під час самих зіткнень.
Для системи двох частинок закон збереження повного імпульсу записується у випадку в такому вигляді:
р 1 + р 2 = р 1 `+ р 2` . (11.29)
Звідси видно, що знаючи будь-які три імпульси, можна визначити четвертий. Наприклад, якщо відомі р 1 р 2 і р 1 `, можна знайти р 2 `, тобто кінцевий імпульс другої частинки:
p 2 `= р 1 + p 2 – p 1 `(11.30)
Так, при ядерному зіткненні, в якому беруть участь два налітають і два ядра, що розлітаються ( хоча система і не є ньютонівською, вважається, що закон збереження повного імпульсу виконується ), імпульс однієї з частинок зазвичай визначається шляхом вимірювання імпульсів інших трьох ядер.
Збереження імпульсу
Тіло, що здійснює механічний рух, має певний імпульс. Це величина, яка має спрямованість (вектор) та визначається за формулою:
p = m × v
При цьому важливо, що напрямок імпульсного вектора тіла, що перебуває в закритій системі, завжди збігається із напрямком (вектором) його швидкості.
Визначення.Якщо сформулювати суть закону збереження імпульсу у вигляді визначення, воно буде звучати наступним чином: векторна сила імпульсів сукупності тіл закритої системи є постійною величиною в тому випадку, якщо сумарна кількість векторів зовнішніх сил, що впливають на систему тіл, дорівнює нулю.
Класична фізика визначає цю закономірність як слідство законів Ньютона. Тож якщо система замкнута і рухається без впливу навколишніх сил, її сумарний імпульс постійний. За наявності стороннього силового впливу імпульс змінюється залежно від величини та напрямів (векторів) цих сил.
ВизначенняВекторна величина суми імпульсів, якими володіють тіла, що входять до замкнутої системи, незалежно від властивостей їхньої взаємодії один з одним, постійна.
Другий закон Ньютона, з урахуванням закону збереження імпульсу, можна записати формулою:
F= Δ p ÷ Δ t
Виходячи з цього математичного виразу, коли на тіла, що знаходяться в закритій системі, не виявляється впливу зовнішніх сил (або сумарний їх вплив дорівнює нулю), імпульс тіл у системі незмінний. Математично така закономірність виражається так:
Pk-Pн=0 або Pk = Pн
ПриміткаАналогічна особливість й у проекції напрями сили.
За визначенням закону збереження імпульсу, навіть за змінах імпульсів окремих тіл, що входять до закритої системи, їх сума не змінюється. При цьому можна визначити, з якою швидкістю ті тіла, що взаємодіють, рухаються, навіть якщо не володіти значеннями діючих сил.
Прояв закону збереження імпульсу можна розглянути таку ситуацію.
Дві кулі масами m1 і m2 рухаються назустріч один одному зі швидкостями v 1 і v 2 . Значення їх імпульсів можна визначити за формулами:
Коли відбувається зіткнення, на кожну з куль діє сила, яку слід позначити F1 та F2 .
Звичайно швидкість куль змінюється, що веде до зміни значення імпульсів.
Однак, в результаті застосування закону, що розглядається, можна записати рівність:
P1+P2=P1′ +P2′
Таким чином, закон збереження імпульсу має ще одне формулювання:
ВизначенняВекторне значення суми імпульсів тіл, які входять у замкнуту систему, є величиною постійної за умови відсутності впливу сторонніх сил чи сума їх векторів дорівнює нулю.
За яких умов виконується закон застосування імпульсу
Відсутність змін у сумі імпульсів тіл замкнутої системи проявляється у тому випадку, коли на них не діють зовнішні сили . Це обов’язкова умова, оскільки інакше швидкості учасників процесу змінюватимуться, а отже, значення імпульсів та їх суми не залишаться постійними.
За більш детального розгляду цієї умови, вона може бути доповнена. Відсутність замкнутості системи допускається у випадках:
- коли сума векторів сил, що впливають, дорівнює нулю;
- сума проекцій, що впливають ззовні сил на обрану вісь координат, дорівнює нулю.
Ще однією умовою, за якої зовнішніми силами можна знехтувати, є незначність часу їхнього впливу . Прикладом може бути постріл, вибух, удар. Тоді, незважаючи на наявність зовнішньої сили, систему тіл, що взаємодіють, можна вважати замкненою.